Let’s take a look how how CLRG does its scoring! With math!
How CLRG Scoring Works
As I am given to understand, the scoring works like so:
- Adjudicators give you a “raw score”: a real number between 0 and 100
- The scoring system ranks each dancer per adjudicator, based on raw scores
- These rankings are mapped into “award points”
- All of a dancer’s award points are summed
- Final ranking is determined by comparing total award points
Raw Scoring
The way raw scores translate into rankings and award points is a little confusing, so I’ve made a little tool you can play with to get a feel for how it works. Essentially, it’s a way of normalizing places to an adjudicator: score weights are only relative to the judge that assigns them.
Adjudicator A can assign scores between 80 and 100; adjudicator B can assign scores between 1 and 40; and they’ll both have a first, second, third, fourth place, etc. These places then get translated into award points.
Award Points
Award points are handed out based on ranking against other dancers for that adjudicator. I obtained these values from a FeisWorx results page for my kid:
| Ranking | Award Points |
|---|
If there’s a 2-way, 3-way, or n-way tie, all tied dancers get the average of the next 2, 3, or n award points, and the next 2, 3, or n rankings are skipped.
What’s with these values?
At first glance, the award points look like the output of an exponential function.
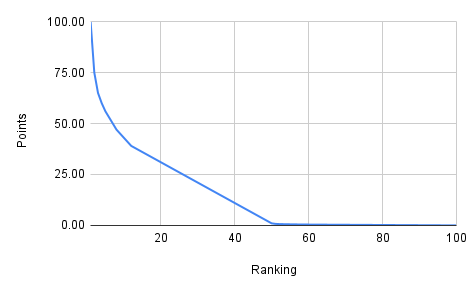
In an effort to figure out where these numbers came from, I ran some curve fitting against the data. Here’s the best I could come up with:
| Ranking range | Award Points Function | Type of function |
|---|---|---|
| 1 - 11 | 100 * x^-0.358 | Exponential |
| 12 - 50 | 51 - x | Linear |
| 51 - 60 | 14.2 - 0.46x + 0.00385x | Polynomial |
| 61 - 100 | 1 - x/100 | Linear |
If you, dear reader, are a mathematician, I would love to hear your thoughts on why they went with this algorithm.
There are a few points to note here:
- 1st place is a huge deal. Disproportionately huge.
- Places 2-10 are similarly big deals compared to places 3-11.
- Places 12-50 operate the way most people probably assume ranking works: linearly.
- Places 51-60 fit best to a second degree polynomial, but it doesn’t matter much for differences of hundreths of a point. This section is really weird, mathematically.
- Places 61-100 are all less than 1 point. If you’re a judge trying to tank a top dancer, anywhere in this range is equivalent to anywhere else.
Consequences of Exponential Award Points
Playing around with this, I’ve found a few interesting consequences of the exponential growth in the top 11 places.
1st place is super important
1st place is weighted so heavily that one judge could move a 5th place dancer into 2nd.
| Alice | Bob | Carol | |
|---|---|---|---|
| Adj. 1 | |||
| Adj. 2 | |||
| Adj. 3 | |||
| Award Points | |||
| Ranking |
You can adjust these values to get a better feel for how scoring works.
Tanking a high-ranked dancer is another way to cheat
Because of that exponential curve, a low ranking from a single judge can carry a lot of weight.
| Alice | Bob | Carol | |
|---|---|---|---|
| Adj. 1 | |||
| Adj. 2 | |||
| Adj. 3 | |||
| Award Points | |||
| Ranking |
Being in 1st provides a nice buffer
Try playing around with Alice’s rankings with Adjudicators 2 and 3 here. She has to get ranked a lot lower before her overall ranking starts going down.
| Alice | Bob | Carol | Dave | Erin | |
|---|---|---|---|---|---|
| Adj. 1 | |||||
| Adj. 2 | |||||
| Adj. 3 | |||||
| Award Points | |||||
| Ranking |